A fontosabb gráf-algoritmusok
A gráfokon különféle algoritmusokat végezhetünk el, ehhez pedig először egy konkrét, objektum-orientált adatszerkezetet kell definiálnunk:
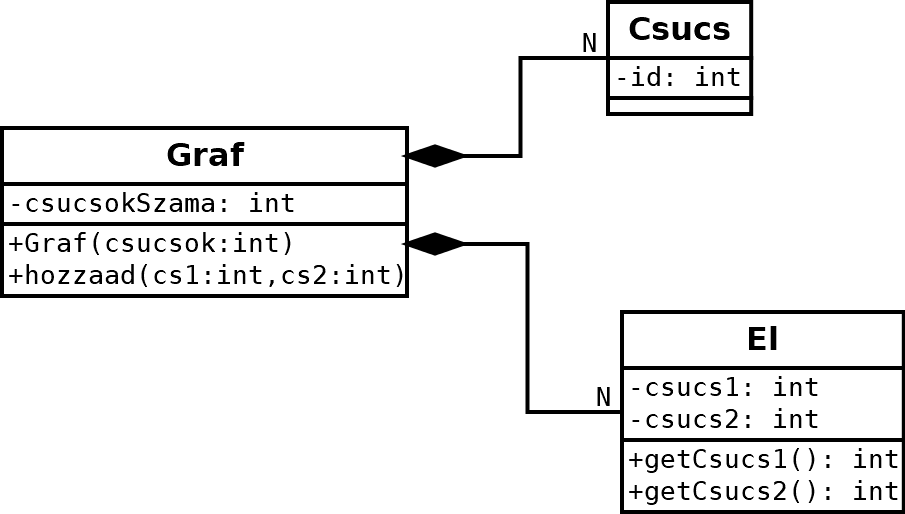
A gráf külső iterfészét a Graf osztály fogja jelenteni. Az ehhez tartozó metódusokkal fogjuk a gráfot kezelni, az algoritmusokat lefuttatni - a gráf használójának nem kell tudni a belső felépítésről, a Csucs és El osztályokról.
A tárolás módja éllista lesz, ahol minden élt az El osztály egy példánya fogja jelenteni. A könnyebb kezelhetőség kedvéért az élt úgy tároljuk el, hogy mindkét irányt felvesszük, vagyis ha szerepel az 1-3 él, akkor a 3-1 is szerepelni fog.
Emellett még eltároljuk a gráf csúcsait is egy-egy objektumban.
Ezt a két osztályt a későbbiekben ki lehet egészíteni, ha egy-egy élhez vagy csúcshoz még további adatot szeretnénk eltárolni.
A gráf egyszerű és irányítatlan lesz, de egyéb adatokkal (pl. súly, szín) ki lehet egészíteni.
A kontruktorban előre meg kell adni a csúcsok számát, ez később nem módosítható. Kezdetben a gráf egy élt sem tartalmaz.
A hozzad függvény segíségével adhatunk hozzá új éleket, a csúcs indexek (0 … N-1) megadásával. Törlésre jelenleg nincs mód.
A fenti osztályt az alábbi három példa-projekt meg is valósítja:
Bejárás
Egy gráfot kétféleképp lehet bejárni. Kiválasztunk egy kezdőpontot, aztán:
- Széllességben folytatjuk
- Először megvizsgáljuk a pont összes szomszédját
- Majd azoknak az összes szomszédját
- Stb.
- Ezen az oldalon az első ábra rendkívül jól illusztrálja
- Mélységben folytatjuk
- Először megvizsgáljuk a pont egy szomszédját
- Majd annak egy szomszédját
- Ha nem tudunk tovább menni, visszalépünk, és a pont egy másik szomszédjával folytatjuk
- Ha elfogy, megint visszalépünk
- Ha a kezdőponból is visszalépnénk, végeztünk
- Ezen az oldalon az első pár ábra rendkívül jól illusztrálja
A szélességi bejárás algoritmusa
A szélességi bejárásnál az elemeket egy sor adatszerkezetbe fűzzük, majd ebből kivéve vizsgáljuk az elemeket és a szomszédjaikat.
Gráf.SzelességiBejár(kezdopont: egész):
// Kezdetben egy pontot sem jártunk be
bejárt = új üres Halmaz()
// A következőnek vizsgált elem a kezdőpont
következők = új üres Sor()
következők.hozzáad(kezdőpont)
bejárt.hozzáad(kezdőpont)
// Amíg van következő, addig megyünk
Ciklus amíg következők nem üres:
// A sor elejéről vesszük ki
k = következők.kivesz()
// Elvégezzük a bejárási műveletet, pl. a konzolra kiírást:
Kiír(this.csúcsok[k])
Ciklus él = this.élek elemei:
// Megkeressük azokat az éleket, amelyek k-ból indulnak
// Ha az él másik felét még nem vizsgáltuk, akkor megvizsgáljuk
Ha (él.csúcs1 == k) és (bejárt nem tartalmazza él.csúcs2-t):
// A sor végére és a bejártak közé szúrjuk be
következők.hozzáad(él.csúcs2)
bejárt.hozzáad(él.csúcs2)
// Jöhet a sor szerinti következő elem
A mélységi bejárás bejárás algoritmusa (1. változat)
Szinte teljes mértékben megegyezik a szélességi bejárással. A különbség, hogy a sor helyet verem adatszerkezetbe tesszük a pontokat:
Gráf.MélységiBejár(kezdopont: egész):
// Kezdetben egy pontot sem jártunk be
bejárt = új üres Halmaz()
// A következőnek vizsgált elem a kezdőpont
következők = új üres Verem()
következők.hozzáad(kezdőpont)
bejárt.hozzáad(kezdőpont)
// Amíg van következő, addig megyünk
Ciklus amíg következők nem üres:
// A verem tetejéről vesszük le
k = következők.kivesz()
// Elvégezzük a bejárási műveletet, pl. a konzolra kiírást:
Kiír(this.csúcsok[k])
Ciklus él = this.élek elemei:
// Megkeressük azokat az éleket, amelyek k-ból indulnak
// Ha az él másik felét még nem vizsgáltuk, akkor megvizsgáljuk
Ha (él.csúcs1 == k) és (bejárt nem tartalmazza él.csúcs2-t):
// A verem tetejére és a bejártak közé adjuk hozzá
következők.hozzáad(él.csúcs2)
bejárt.hozzáad(él.csúcs2)
// Jöhet a sor szerinti következő elem
A mélységi bejárás bejárás algoritmusa (2. változat)
A verem helyett a hívási stack-et is felhasználhatjuk, így egy könnyebben megérthető, rekurzív algoritmust kapunk:
// A fő függvény, amivel a rekurziót elindítjuk
Graf.MélységiBejár(kezdőpont: egész):
bejárt = új üres Halmaz()
bejárt.hozzáad(kezdőpont)
this.MélységiBejárRekurzív(k, bejárt)
// Segédfüggvény, amely magát a rekurziót végzi
Gráf.MélységiBejárRekurzív(k: egész, bejárt: Halmaz):
// Elvégezzük a bejárási műveletet, pl. a konzolra kiírást:
Kiír(this.csúcsok[k])
Ciklus él = this.élek elemei:
// Megkeressük azokat az éleket, amelyek k-ból indulnak
// Ha az él másik felét még nem vizsgáltuk, akkor megvizsgáljuk
Ha (él.csúcs1 == k) és (bejárt nem tartalmazza él.csúcs2-t):
bejárt.hozzáad(él.csúcs2)
Gráf.MélységiBejárRekurzív(él.csúcs2, bejárt)
Összefüggőség
Az összefüggőség vizsgálatához a gráfot be kell járni egy tetszőleges pontból, tetszőleges módszerrel. Ha minden elemet bejártunk, akkor a gráf összefüggő.
Úgy is elképzelhetjük, mint egy képszerkesztő alkalmazásban a flood fill eszközt: ha kimarad egy elem, akkor nem összefüggő, ha pedig az egészet sikerül beszínezni, akkor összefüggő.
Alakítsuk át egy picit mondjuk a szélességi bejárás algoritmusát:
Gráf.Összefüggő(): logikai
bejárt = új üres Halmaz()
következők = új üres Sor()
következők.hozzáad(0) // Tetszőleges, mondjuk 0 kezdőpont
bejárt.hozzáad(0)
Ciklus amíg következők nem üres:
k = következők.kivesz()
// Bejárás közben nem kell semmit csinálni
Ciklus él = this.élek elemei:
Ha (él.csúcs1 == k) és (bejárt nem tartalmazza él.csúcs2-t):
következők.hozzáad(él.csúcs2)
bejárt.hozzáad(él.csúcs2)
// A végén megvizsgáljuk, hogy minden pontot bejártunk-e
Ha bejárt.elemszám == this.csúcsokSzáma:
Vissza: igaz
Különben:
Vissza: hamis
Feszítőfa készítése
A feszítőfa egy olyan fa, amely a pontosan az eredeti gráf pontjait tartalmazza, de az elék közül csak azokat, amelyekkel még fa (azaz körmentes) lesz a gráf.
Az algoritmus módszere, hogy egy bejárási algoritmus lényegében egy fát ír le - mindössze meg kell jegyeznünk, hogy melyik él mentén haladtunk végig. Ha olyan pontba futunk, amit már vizsgáltunk, akkor azt az élt már nem vesszük figyelembe, mert kört okozna.
Az algoritmus nyilván csak akkor ad helyes eredményt, ha a gráf összefüggő.
Gráf.Feszitőfa(): Gráf
// Új, kezdetben él nélküli gráf
fa = új Gráf(this.csúcsokSzáma)
// Bejáráshoz szükséges adatszerkezetek
bejárt = új üres Halmaz()
következők = új üres Sor()
// Tetszőleges, mondjuk 0 kezdőpont
következők.hozzáad(0)
bejárt.hozzáad(0)
// Szélességi bejárás
Ciklus amíg következők nem üres:
aktuálisCsúcs = következők.kivesz()
Ciklus él = this.élek elemei:
Ha él.csúcs1 == aktuálisCsúcs:
Ha bejárt nem tartalmazza él.Csúcs2-t
bejárt.hozzáad(él.csúcs2)
következők.hozzáad(él.Csúcs2)
// A fába is vegyük bele az élt
fa.hozzáad(él.Csucs1, él.csúcs2)
// Az eredményül kapott gráf az eredeti gráf feszítőfája
vissza: fa
Csúcs-színezés mohó algoritmussal
A feladat lényege, hogy mindn csúcsot úgy kell egy adott színre színezni, hogy az egymással szomszédos csúcsok ne legyenen egyszínűek. Gondoljunk egy térképre: a szomszédos országok különböző színűek.
Az algoritmus attól mohó, hogy nem gondolkodik előre, nem foglalkozik azzal, hogy a lehető legkevesebb színt használja fel.
Az algoritmus kimenete egy (csúcs: egész) => (szín: egész) szótár lesz. A színt is 0…N-1 közötti egész számokkal jelöljük.
Gráf.MohóSzínezés(): Szótár(egész => egész)
színezés = új üres Szótár()
// Legrosszabb esetben minden csúcsot különböző színűre kell színezni,
// ezért ennyi szín elég lesz
maxSzín = this.csúcsokSzáma
Ciklus aktuálisCsúcs = 0-tól this.csúcsokSzáma - 1 -ig:
// Kezdetben bármely színt választhatjuk
választhatóSzínek = új Halmaz(), amely
0...maxSzín-1 elemekkel van feltöltve
// Vizsgáljuk meg a szomszédos csúcsokat:
Ciklus él = this.élek elemei:
Ha él.csúcs1 == aktuálisCsúcs:
// Ha a szomszédos csúcs már be van színezve,
// azt a színt már nem választhatjuk
Ha színezés.tartalmazKulcsot(él.csúcs2):
szín = színezés[él.csúcs2]
választhatóSzínek.kivesz(szín)
// A maradék színekből válasszuk ki a legkisebbet
választottSzín = Min(választhatóSzínek)
színezés.hozzáad(aktuálisCsúcs, választottSzín)
vissza: színezés
Útkeresés - Dijkstra
Az útkeresés azt az algoritmust jelöli, hogy egy adott keződőpontból hogyan lehet eljutni az összes többi pontba, a lehető legrövidebb idő (legkisebb súly) felhasználásával.
Ehhez a gráfunkat ki kell egészíteni, hogy az élek tartalmazzanak egy súly tulajdonságot is:
Él osztály:
csúcs1: egész
csúcs2: egész
súly: lebegőpontos, > 0
Az útkeresés Dijkstra algoritmusával fog történni. Egy segédosztályt is definiálunk, amiben az átmeneti, ill. a végeredményt tároljuk. Minden csúcshoz egy ilyen objektum fog tartozni:
CsúcsAdat osztály:
// Ebből a csúcsból érkeztünk
forrásCsúcs: egész = -1
// Ennyi a minimun költség, kezdetben végtelen
költség: lebegőpontos = végtelen
// Már vizsgáltuk-e:
vizsgáltuk: logikai = hamis
Az algoritmus kimenete egy szótár, minden csúcshoz hozzárendeli a csúcshoz tartozó költséget, és hogy ahhoz a csúcshoz hogyan lehet eljutni.
Gráf.Dijkstra(kezdőpont: egész): Szótár(egész => CsúcsAdat)
csúcsAdatok = új Szótár()
Ciklus csúcsIndex = 0-tól this.csúcsokSzáma-1 -ig:
csúcsAdatok.hozzáad(csúcsIndex, új CsúcsAdat())
// A kezdőpont költsége 0, hiszen innen indulunk:
csúcsAdatok[kezdőpont].költség = 0
// Minden csúcsot megvizsgálunk, de nem a szokványos sorrendben
vizsgáltDarab = 0
Ciklus amíg vizsgáltDarab < this.csúcsokSzáma:
vizsgáltDarab++
// Segédfüggvény, amely kiválasztja a következő csúcst
// l. lentebb
vizsgáltCsúcs = this.KövetkezőCsúcs(csúcsAdatok)
csúcsAdatok[vizsgáltCsúcs].vizsgáltuk = igaz
// Vizsgáljuk meg a szomszédos csúcsokat:
Ciklus él = this.élek elemei:
Ha él.csúcs1 == aktuálisCsúcs:
// Ha ezen a csúcson keresztül szeretnénk
// a másik csúcsba eljutni, akkor
// ennyibe kerülne:
újKöltség = csúcsAdatok[vizsgáltCsúcs].költség + él.súly
// Ha az kisebb, akkor javítsunk az úton:
Ha újKöltség < csúcsAdatok[él.csúcs2].költség:
csúcsAdatok[él.csúcs2].költség = újKöltség
csúcsAdatok[él.csúcs2].forrásCsúcs = aktuálisCsúcs
// Ha minden elemet megvizsgáltunk, akkor a szótárunk
// tartalmazni fogja a költségeket és az útvonalat
vissza: csúcsAdatok
// A következő csúcs a legkisebb költségű lesz,
// de csak akkor, ha még nem vizsgáltuk
Gráf.KövetkezőCsúcs(csúcsAdatok): egész
minIndex = index:
Ciklus index, adat = csúcsAdatok elemei:
Ha (adat.vizsgáltuk == hamis) és
(adat.költség < csúcsAdatok[minIndex].költség):
minIndex = index
vissza: minIndex
Példa
Vegyük az alábbi gráfot:
Az algoritmus végeredménye egy ehhez hasonló táblázat lesz, a kiindulópont itt az 1-es index volt:
| kulcs | forrásCsúcs | költség | vizsgáltuk |
|---|---|---|---|
| 0 | 1 | 1 | igaz |
| 1 | -1 | 0 | igaz |
| 2 | 3 | 7 | igaz |
| 3 | 1 | 5 | igaz |
| 4 | 2 | 11 | igaz |
Az első oszlop a szótár kulcsa, a többi az objektum értékei.
A forrásCsúcs oszlopot visszakövetve kinyerhetjük, hogy milyen úton jutottunk el pl. a 4-es pontba:
- A 4 a célpont: [4]
- 4-nek a forráscsúcsa 2: [2, 4]
- 2-nek a forráscsúcsa 3: [3, 2, 4]
- 3-nak a forráscsúcsa 1: [1, 3, 2, 4]
- Az 1 a kezdőpont, végeztünk
Az 1-ből 4-be a legkisebb költségű út az 1-3-2-4 élsorozat, a költsége 11.
Bármely útkeresési algoritmus csak pozitív súlyokkal működik helyesen. Ha negatív súlyt is felvennénk, akkor az adott élen oda-vissza járva tetszőlegesen le lehetne csökkenteni a költséget, aminek nincs gyakorlati értelme.
